1. Ydinkaavan fysikaalisen periaatteen todentaminen
Massan säilymisen laki
Kaikki kaavat perustuvat yhtälön m=ρ×V (massa = tiheys × tilavuus) fysikaaliseen luonteeseen
Tiheysarvo
Puhtaan alumiinin teoreettinen tiheys: 2 698 kg/m³ (20 ℃)
Arvioitu arvo 2 700 kg/m³ on kohtuullinen teollisuuslaskelmiin (virhe < 0,1 %).
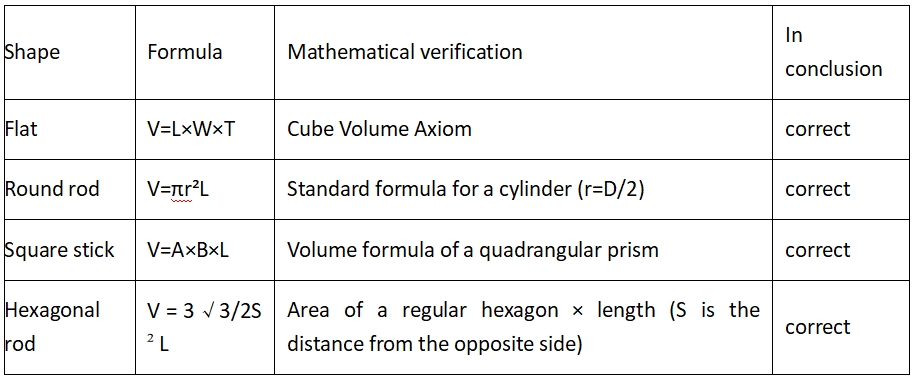
2. Geometristen kaavojen tarkkuuden varmentaminen
2.1. Standardi geometrinen tilavuuskaava
Neliöputken kaavan rajoitukset:
Tämä pätee, kun putken seinämän paksuus on tasainen ja sisäkulma on suorakulmainen (varsinaisessa neliöputkessa on pyöristetty siirtymä ja teoreettinen virhe on noin 1–3 %).
3. Yksikköjärjestelmän yhdenmukaisuuden varmennus
Yksiköiden välinen laskenta riskipisteiden tutkinnassa
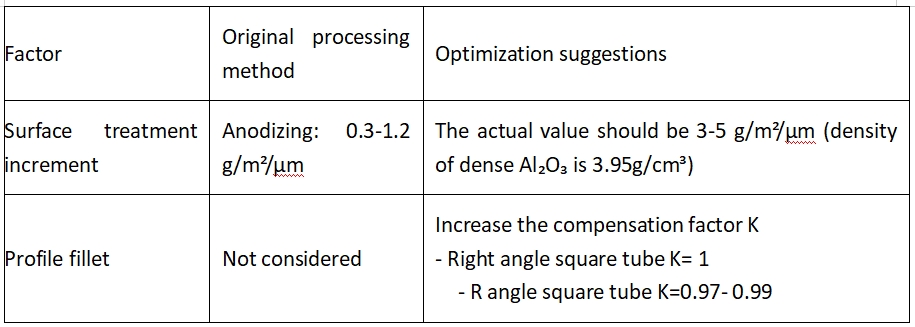
4. Teknisen soveltuvuuden tarkistus
4.1. Epäideaalisten tekijöiden kompensointi
4.2. Toleranssin vaikutuksen kvantifiointi
Paksuustoleranssi ±10 % → Painopoikkeama ±(8 % ~ 12 %) (ohutseinäiset osat ovat herkempiä)
Ratkaisu: W todellinen = W teoreettinen × (1 + Δt / t) (Δt : paksuuspoikkeama)
5. Reunaehtojen testi
Äärimmäisen tapauksen varmennus:
Tiheyspoikkeaman skenaario
7xxx-seos (7075): Mitattu tiheys 2,810 g/cm³ → Jos vahingossa käytetään tiheyttä 2,7 g/cm³, virhe on +4,1 %.
Kaavataulukko
4t(A + B)- 4t² on vakiomuotoinen tekninen laskelma, joka lasketaan kertomalla poikkileikkauksen kehä seinämän paksuudella ja vähentämällä sitten neljä kulmaa.
Laskelmaesimerkki:
1.6061 alumiinilevy(1000 × 500 × 10 mm, pituus 2 m): L = 1000 × 500 × 2 × 0,0027 = 27 kg
2.7075 pyöreä putki(ulkohalkaisija 50 mm, seinämän paksuus 3 mm, pituus 1,5 m): W = [(50-3)×3×3,1416×1,5]×0,00283 ≈ 5,65 kg
3. Neliöputki(40 × 40 × 2 mm, pituus 3 m): W = [2 × 2 × (40 + 40 - 4) × 3] × 0,0027 × 0,98 ≈ 2,42 kg
Suositeltu työnkulku
1. Valitse tiheys → 2. Mittaa todellinen koko → 3. Valitse kompensaatiokerroin → 4. Laske kaavalla
Julkaisun aika: 17. kesäkuuta 2025